Conceptos Básicos del Análisis LR

Los analizadores generados por jison entran en la categoría de analizadores LR. Estos analizadores construyen una derivación a derechas inversa (o antiderivación). De ahí la R en LR (del inglés rightmost derivation). El árbol sintáctico es construido de las hojas hacia la raíz, siendo el último paso en la antiderivación la construcción de la primera derivación desde el símbolo de arranque.

Empezaremos entonces considerando las frases que pueden aparecer en una derivación a derechas. Tales frases consituyen el lenguaje de las formas sentenciales a derechas $FSD$:

Definición 5.5.1   Dada una gramática $G =(\Sigma,V,P,S)$ no ambigua, se denota por $FSD$ (lenguaje de las formas Sentenciales a Derechas) al lenguaje de las sentencias que aparecen en una derivación a derechas desde el símbolo de arranque.

$FSD = \left \{ \alpha \in (\Sigma \cup V)* : \exists S \begin{array}{c} * \Longrightarrow {\scriptstyle RM} \end{array} \alpha \right \}$

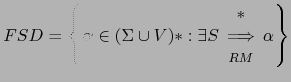
Donde la notacion RM indica una derivación a derechas (rightmost). Los elementos de $FSD$ se llaman ``formas sentenciales derechas''.

Dada una gramática no ambigua $G =(\Sigma,V,P,S)$ y una frase $x \in L(G)$ el proceso de antiderivación consiste en encontrar la última derivación a derechas que dió lugar a $x$. Esto es, si $x \in L(G)$ es porque existe una derivación a derechas de la forma

$S \stackrel{*}{\Longrightarrow} y A z \Longrightarrow y w z = x$.

El problema es averiguar que regla $A \rightarrow w$ se aplicó y en que lugar de la cadena $x$ se aplicó. En general, si queremos antiderivar una forma sentencial derecha $\beta \alpha w$ debemos averiguar por que regla $A \rightarrow \alpha$ seguir y en que lugar de la forma (después de $\beta$ en el ejemplo) aplicarla.

$S \stackrel{*}{\Longrightarrow} \beta A w \Longrightarrow \beta \alpha w$.

La pareja formada por la regla y la posición se denomina handle, mango o manecilla de la forma. Esta denominación viene de la visualización gráfica de la regla de producción como una mano que nos permite escalar hacia arriba en el árbol. Los ``dedos'' serían los símbolos en la parte derecha de la regla de producción.

Definición 5.5.2   Dada una gramática $G =(\Sigma,V,P,S)$ no ambigua, y dada una forma sentencial derecha $\alpha = \beta \gamma x$, con $x \in \Sigma^*$, el mango o handle de $\alpha$ es la última producción/posición que dió lugar a $\alpha$:

$S \begin{array}{c} * \Longrightarrow {\scriptstyle RM} \end{array} \beta B x \Longrightarrow \beta \gamma x = \alpha$

Escribiremos: $handle(\alpha) = (B \rightarrow \gamma, \beta \gamma)$. La función $handle$ tiene dos componentes: $handle_1(\alpha) = B \rightarrow \gamma$ y $handle_2(\alpha) = \beta \gamma$

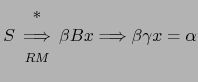
Si dispusieramos de un procedimiento que fuera capaz de identificar el mango, esto es, de detectar la regla y el lugar en el que se posiciona, tendríamos un mecanismo para construir un analizador. Lo curioso es que, a menudo es posible encontrar un autómata finito que reconoce el lenguaje de los prefijos $\beta \gamma$ que terminan en el mango. Con mas precisión, del lenguaje:

Definición 5.5.3   El conjunto de prefijos viables de una gramática G se define como el conjunto:

$PV = \left \{ \delta \in (\Sigma \cup V)* : \exists S \begin{array}{c} * \Lo... ...mbox{ y }\delta es un prefijo de handle_2(\alpha) = \beta \gamma \right \}$

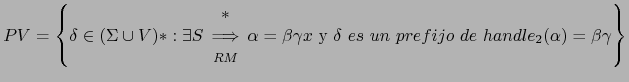
Esto es, es el lenguaje de los prefijos viables es el conjunto de frases que son prefijos de $handle_2(\alpha)) = \beta \gamma$, siendo $\alpha$ una forma sentencial derecha ( $\alpha \in FSD$). Los elementos de $PV$ se denominan prefijos viables.

Obsérvese que si se dispone de un autómata que reconoce $PV$ entonces se dispone de un mecanismo para investigar el lugar y el aspecto que pueda tener el mango. Si damos como entrada la sentencia $\alpha = \beta \gamma x$ a dicho autómata, el autómata aceptará la cadena $\beta \gamma$ pero rechazará cualquier extensión del prefijo. Ahora sabemos que el mango será alguna regla de producción de $G$ cuya parte derecha sea un sufijo de $\beta \gamma$.

Definición 5.5.4   El siguiente autómata finito no determinista puede ser utilizado para reconocer el lenguaje de los prefijos viables PV:

• Alfabeto = $V \cup \Sigma$
• Los estados del autómata se denominan LR(0) items. Son parejas formadas por una regla de producción de la gramática y una posición en la parte derecha de la regla de producción. Por ejemplo, $(E \rightarrow E + E, 2)$ sería un LR(0) item para la gramática de las expresiones.

  Conjunto de Estados:

  $Q = \left \{ (A \rightarrow \alpha, n) : A \rightarrow \alpha \in P, n \le \vert\alpha\vert \right \}$

  La notación $\mid \alpha \mid$ denota la longitud de la cadena $\mid \alpha \mid$. En vez de la notación $(A \rightarrow \alpha, n)$ escribiremos: $A \rightarrow \beta _\uparrow \gamma$ $= \alpha$, donde la flecha ocupa el lugar indicado por el número $n = \mid \beta \mid$ :

• La función de transición intenta conjeturar que partes derechas de reglas de producción son viables. El conjunto de estados actual del NFA representa el conjunto de pares (regla de producción, posición en la parte derecha) que tienen alguna posibilidad de ser aplicadas de acuerdo con la entrada procesada hasta el momento:
  $\delta(A \rightarrow \alpha _\uparrow X \beta, X) = A \rightarrow \alpha X _\uparrow \beta \forall X \in V \cup \Sigma$
  $\delta(A \rightarrow \alpha _\uparrow B \beta, \epsilon) = B \rightarrow _\uparrow \gamma \forall B \rightarrow \gamma \in P$

• Estado de arranque: Se añade la superregla $S' \rightarrow S$ a la gramática $G =(\Sigma,V,P,S)$. El LR(0) item $S' \rightarrow _\uparrow S$ es el estado de arranque.
• Todos los estados definidos (salvo el de muerte) son de aceptación.

Denotaremos por $LR(0)$ a este autómata. Sus estados se denominan $LR(0)-items$. La idea es que este autómata nos ayuda a reconocer los prefijos viables $PV$.

Una vez que se tiene un autómata que reconoce los prefijos viables es posible construir un analizador sintáctico que construye una antiderivación a derechas. La estrategia consiste en ``alimentar'' el autómata con la forma sentencial derecha. El lugar en el que el autómata se detiene, rechazando indica el lugar exacto en el que termina el handle de dicha forma.

Ejemplo 5.5.1   Consideremos la gramática:

S $\rightarrow$ a S b

S $\rightarrow$ $\epsilon$

El lenguaje generado por esta gramática es $L(G) = \{ a^n b^n : n \ge 0 \}$ Es bien sabido que el lenguaje $L(G)$ no es regular. La figura 5.1 muestra el autómata finito no determinista con $\epsilon$-transiciones (NFA) que reconoce los prefijos viables de esta gramática, construido de acuerdo con el algoritmo 5.5.4.

Véase https://github.com/crguezl/jison-aSb para una implementación en Jison de una variante de esta gramática.

Figura 5.1: NFA que reconoce los prefijos viables

Ejercicio 5.5.1   Simule el comportamiento del autómata sobre la entrada $aabb$. ¿Donde rechaza? ¿En que estados está el autómata en el momento del rechazo?. ¿Qué etiquetas tienen? Haga también las trazas del autómata para las entradas $aaSbb$ y $aSb$. ¿Que antiderivación ha construido el autómata con sus sucesivos rechazos? ¿Que terminales se puede esperar que hayan en la entrada cuando se produce el rechazo del autómata?