Subsecciones
Conceptos Básicos para el Análisis Sintáctico
Suponemos que el lector de esta sección ha realizado con éxito
un curso en teoría de autómatas y lenguajes formales.
Las siguientes definiciones repasan los conceptos mas importantes.
Definición 5.1.2
Una gramática 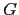 es una cuaterna
es una cuaterna
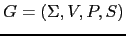 .
.
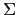 es el conjunto de terminales.
es el conjunto de terminales. 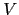 es un conjunto (disjunto de
es un conjunto (disjunto de 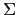 )
que se denomina conjunto de variables sintácticas o categorías gramáticales,
P es un conjunto de pares de
)
que se denomina conjunto de variables sintácticas o categorías gramáticales,
P es un conjunto de pares de
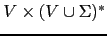 . En vez de escribir
un par usando la notación
. En vez de escribir
un par usando la notación
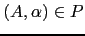 se escribe
se escribe
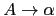 .
Un elemento de
.
Un elemento de 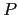 se denomina producción. Por último,
se denomina producción. Por último, 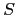 es un símbolo del conjunto
es un símbolo del conjunto
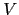 que se denomina símbolo de arranque.
que se denomina símbolo de arranque.
Definición 5.1.6
Observe que una derivación puede ser representada como un árbol cuyos nodos
están etiquetados en
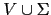 . La aplicación de la regla de
producción
. La aplicación de la regla de
producción
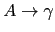 se traduce en asignar como hijos del nodo etiquetado con
se traduce en asignar como hijos del nodo etiquetado con 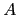 a los nodos etiquetados con los símbolos
a los nodos etiquetados con los símbolos
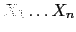 que constituyen
la frase
que constituyen
la frase
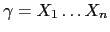 .
Este árbol se llama árbol sintáctico concreto asociado
con la derivación.
.
Este árbol se llama árbol sintáctico concreto asociado
con la derivación.
Definición 5.1.7
Observe que, dada una frase
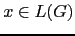 una derivación desde el
símbolo de arranque da lugar a un árbol. Ese árbol tiene como raíz el
símbolo de arranque y como hojas los terminales
una derivación desde el
símbolo de arranque da lugar a un árbol. Ese árbol tiene como raíz el
símbolo de arranque y como hojas los terminales
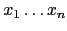 que forman
que forman 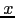 . Dicho árbol se denomina árbol
de análisis sintáctico concreto de
. Dicho árbol se denomina árbol
de análisis sintáctico concreto de 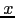 . Una derivación determina
una forma de recorrido del árbol de análisis sintáctico concreto.
. Una derivación determina
una forma de recorrido del árbol de análisis sintáctico concreto.
Definición 5.1.8
Una gramática 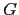 se dice ambigua si existe alguna frase
se dice ambigua si existe alguna frase
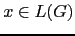 con al menos dos árboles sintácticos.
Es claro que esta definición es equivalente a afirmar que existe
alguna frase
con al menos dos árboles sintácticos.
Es claro que esta definición es equivalente a afirmar que existe
alguna frase
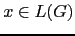 para la cual existen dos derivaciones a
izquierda (derecha) distintas.
para la cual existen dos derivaciones a
izquierda (derecha) distintas.
Ejercicio
Dada la gramática con producciones:
program
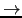 declarations statements declarations statements 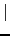 statements statements |
declarations
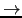 declaration ';' declarations declaration ';' declarations 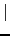 declaration ';' declaration ';' |
declaration
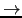 INT idlist INT idlist 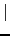 STRING idlist STRING idlist |
statements
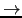 statement ';' statements statement ';' statements 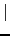 statement statement |
statement
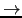 ID '=' expression ID '=' expression 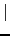 P expression P expression |
expression
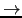 term '+' expression term '+' expression 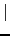 term term |
term
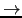 factor '*' term factor '*' term 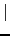 factor factor |
factor
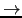 '(' expression ')' '(' expression ')' 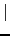 ID ID 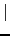 NUM NUM 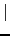 STR STR |
idlist
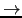 ID ',' idlist ID ',' idlist 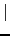 ID ID |
En esta gramática, 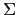 esta formado por los caracteres entre comillas simples y
los símbolos cuyos identificadores están en mayúsculas. Los restantes identificadores
corresponden a elementos de
esta formado por los caracteres entre comillas simples y
los símbolos cuyos identificadores están en mayúsculas. Los restantes identificadores
corresponden a elementos de 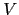 . El símbolo de arranque es
. El símbolo de arranque es
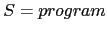 .
.
Conteste a las siguientes cuestiones:
- Describa con palabras el lenguaje generado.
- Construya el árbol de análisis sintáctico
concreto para cuatro frases del lenguaje.
- Señale a que recorridos del árbol corresponden las respectivas
derivaciones a izquierda y a derecha en el apartado 2.
- ¿Es ambigua esta gramática?. Justifique su respuesta.
Casiano Rodríguez León
2016-03-27


![]() , donde
, donde ![]() denota la palabra vacía, esto es
la palabra que tiene longitud cero, formada por cero símbolos del conjunto base
denota la palabra vacía, esto es
la palabra que tiene longitud cero, formada por cero símbolos del conjunto base ![]() .
.![]() esta formado por las cadenas
de terminales que pueden ser derivados desde el símbolo de arranque.
esta formado por las cadenas
de terminales que pueden ser derivados desde el símbolo de arranque.![]() en la cual en cada paso
en la cual en cada paso
![]() la regla de producción aplicada
la regla de producción aplicada
![]() se aplica en la variable sintáctica mas a la derecha se dice una derivación a derechas
se aplica en la variable sintáctica mas a la derecha se dice una derivación a derechas
![]() en la cual en cada paso
en la cual en cada paso
![]() la regla de producción aplicada
la regla de producción aplicada
![]() se aplica en la variable sintáctica mas a la izquierda se dice una derivación a izquierdas
se aplica en la variable sintáctica mas a la izquierda se dice una derivación a izquierdas![]() esta formado por los caracteres entre comillas simples y
los símbolos cuyos identificadores están en mayúsculas. Los restantes identificadores
corresponden a elementos de
esta formado por los caracteres entre comillas simples y
los símbolos cuyos identificadores están en mayúsculas. Los restantes identificadores
corresponden a elementos de ![]() . El símbolo de arranque es
. El símbolo de arranque es
![]() .
.