Subsecciones

Análisis Sintáctico Predictivo Recursivo

La siguiente fase en la construcción del analizador es la fase de análisis sintáctico. Esta toma como entrada el flujo de terminales y construye como salida el árbol de análisis sintáctico abstracto.

El árbol de análisis sintáctico abstracto es una representación compactada del árbol de análisis sintáctico concreto que contiene la misma información que éste.

Existen diferentes métodos de análisis sintáctico. La mayoría caen en una de dos categorías: ascendentes y descendentes. Los ascendentes construyen el árbol desde las hojas hacia la raíz. Los descendentes lo hacen en modo inverso. El que describiremos aqui es uno de los mas sencillos: se denomina método de análisis predictivo descendente recursivo.

Introducción

En este método se asocia una subrutina con cada variable sintáctica $A \in V$ . Dicha subrutina (que llamaremos A) reconocerá el lenguaje generado desde la variable

$L_A(G) = \{ x \in \Sigma^* : A \stackrel{*}{\Longrightarrow} x \}$

En este método se escribe una rutina A por variable sintáctica $A \in V$ . Se le da a la rutina asociada el mismo nombre que a la variable sintáctica asociada. La función de la rutina A asociada con la variable $A \in V$ es reconocer el lenguaje generado por . La estrategia general que sigue la rutina A para reconocer es decidir en términos del terminal en la entrada que regla de producción concreta $A \rightarrow \alpha$ se aplica para a continuación comprobar que la entrada que sigue pertenece al lenguaje generado por $\alpha$ . En un analizador predictivo descendente recursivo (APDR) se asume que el símbolo que actualmente esta siendo observado (denotado lookahead) permite determinar unívocamente que producción de hay que aplicar. Una vez que se ha determinado que la regla por la que continuar la derivación es $A \rightarrow \alpha$ se procede a reconocer $L_{\alpha}(G)$ , el lenguaje generado por $\alpha$ . Si $\alpha = X_1 \ldots X_n$ , las apariciones de terminales en $\alpha$ son emparejadas con los terminales en la entrada mientras que las apariciones de variables en $\alpha$ se traducen en llamadas a la correspondiente subrutina asociada con B.

Para ilustrar el método, simplificaremos la gramática presentada en el ejercicio 34.1.1 eliminando las declaraciones:

statements $\rightarrow$ statement ';' statements $\vert$ statement

statement $\rightarrow$ ID '=' expression $\vert$ P expression

expression $\rightarrow$ term '+' expression $\vert$ term

term $\rightarrow$ factor '*' term $\vert$ factor

factor $\rightarrow$ '(' expression ')' $\vert$ ID $\vert$ NUM

La secuencia de llamadas cuando se procesa la entrada mediante el siguiente programa construye ``implícitamente'' el árbol de análisis sintáctico concreto.

Dado que estamos usando strict se requiere prototipar las funciones al comienzo del fichero:

sub parse();
sub statements();
sub statement();
sub expression();
sub term();
sub factor();
sub idlist();
sub declaration();
sub declarations();

Para saber mas sobre prototipos consulte [10].

Programa 33.6.1

 1 sub match {
 2   my $t = shift;
 3 
 4   if ($lookahead eq $t) {
 5     ($lookahead, $value) = splice @tokens,0,2; 
 6     if (defined($lookahead)) { 
 7       $lookahead = $value if ($lookahead eq 'PUN');
 8     } else { $lookahead = 'EOI'; }
 9   }
10   else { error("Se esperaba $t y se encontro $lookahead\n"); }
11 }
12 
13 sub statement {
14   if ($lookahead eq 'ID') { match('ID'); match('='); expression; }
15   elsif ($lookahead eq 'P') { match('P'); expression; }
16   else { error('Se esperaba un identificador'); }
17 }
18 
19 sub term() {
20   factor;
21   if ($lookahead eq '*') { match('*'); term; }
22 }
23 
24 sub expression() {
25   term;
26   if ($lookahead eq '+') { match('+'); expression; }
27 }
28 
29 sub factor() {
30   if ($lookahead eq 'NUM') { match('NUM'); }
31   elsif ($lookahead eq 'ID') { match('ID'); }
32   elsif ($lookahead eq '(') { match('('); expression; match(')'); }
33   else { error("Se esperaba (, NUM o ID"); }
34 }
35 
36 sub statements {
37   statement;
38   if ($lookahead eq ';') { match(';'); statements; }
39 }
40 
41 sub parser {
42   ($lookahead, $value) = splice @tokens,0,2; 
43   statements; match('EOI');
44 }

Como vemos en el ejemplo, el análisis predictivo confía en que, si estamos ejecutando la entrada del procedimiento A, el cuál está asociado con la variable $A \in V$ , el símbolo terminal que esta en la entrada determine de manera unívoca la regla de producción $A \rightarrow a \alpha$ que debe ser procesada.

Si se piensa, esta condición requiere que todas las partes derechas $\alpha$ de las reglas $A \rightarrow \alpha$ de ``comiencen'' por diferentes símbolos. Para formalizar esta idea, introduciremos el concepto de conjunto $FIRST(\alpha)$ :

Definición 33.6.1 Dada una gramática $G =(\Sigma,V,P,S)$ y un símbolo $\alpha \in (V \cup \Sigma)^*$ se define el conjunto $FIRST(\alpha)$ como:

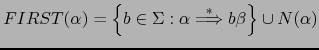
$FIRST(\alpha) = \left \{ b \in \Sigma : \alpha \stackrel{*}{\Longrightarrow} b \beta \right \} \cup N(\alpha)$

donde:

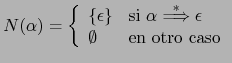
$N(\alpha) = \left \{ \begin{array}{ll} \left \{ \epsilon \right \}& \mbox{si ... ...htarrow} \epsilon$} \\ \emptyset & \mbox{en otro caso} \end{array} \right.$

Podemos reformular ahora nuestra afirmación anterior en estos términos: Si $A \rightarrow \gamma_1 \mid \ldots \mid \gamma_n$ y los conjuntos $FIRST(\gamma_i)$ son disjuntos podemos construir el procedimiento para la variable siguiendo este seudocódigo:

sub A {
  if ($lookahead in FIRST(gamma_1)) { imitar gamma_1 }
  elsif ($lookahead in FIRST(gamma_2)) { imitar gamma_2 }
  ...
  else ($lookahead in FIRST(gamma_n)) { imitar gamma_n }
}

Donde si $\gamma_j$ es $X_1 \ldots X_k$ el código gamma_j consiste en una secuencia $i = 1 \ldots k$ de llamadas de uno de estos dos tipos:

Llamar a la subrutina X_i si es una variable sintáctica
Hacer una llamada a match(X_i) si es un terminal

Ejercicio: Recorrido del árbol en un ADPR

¿En que forma es recorrido el árbol de análisis sintáctico concreto en un analizador descendente predictivo recursivo? ¿En que orden son visitados los nodos?

Ejercicio: Factores Comunes

En el programa 33.6.1 el reconocimiento de las categorías gramáticales statements, expression y term (líneas 19-27) difiere del resto. Observe las reglas:

statements $\rightarrow$ statement ';' statements $\vert$ statement

expression $\rightarrow$ term '+' expression $\vert$ term

term $\rightarrow$ factor '*' term $\vert$ factor

¿Son disjuntos los conjuntos $FIRST(\gamma_i)$ para las partes derechas de las reglas de statements? ¿Son disjuntos los conjuntos $FIRST(\gamma_i)$ para las partes derechas de las reglas de expression? ¿Son disjuntos los conjuntos $FIRST(\gamma_i)$ para las partes derechas de las reglas de term?

Si se tiene una variable con producciones:

$A \rightarrow \alpha \beta \mid \alpha \gamma$

Las dos producciones tienen un máximo factor común en la izquierda de su parte derecha $\alpha$ . Asumimos que $FIRST(\beta) \cap FIRST(\gamma) = \emptyset$ .

¿Cómo puede modificarse la gramática para obtener una nueva gramática que cumpla la condición de que las partes derechas tienen conjuntos $FIRST(\gamma_i)$ disjuntos?
¿Puede modificarse la técnica APDR para que funcione sobre gramáticas con este tipo de producciones?. Observe el código asociado con statements, expression y term. ¿Cómo sería el esquema general?

Derivaciones a vacío

Surge un problema cuando $A \rightarrow \gamma_1 \mid \ldots \mid \gamma_n$ y la palabra vacía está en alguno de los conjuntos $FIRST(\gamma_i)$ . ¿Que hacer entonces?

Nótese que si $A \rightarrow \gamma$ y $\epsilon \in FIRST(\gamma)$ es porque existe una derivación $\gamma \stackrel{*}{\Longrightarrow} \epsilon$ . ¿Que terminales podemos legalmente encontrarnos cuando estamos en la subrutina A? Consideremos una derivación desde el símbolo de arranque en la que se use la producción $A \rightarrow \gamma$ . Dicha derivación forzosamente tendrá la forma:

$S \stackrel{*}{\Longrightarrow} \beta A a \mu \Longrightarrow \beta \gamma a \mu \stackrel{*}{\Longrightarrow} \beta a \mu$ .

Cualquier terminal $a \in \Sigma$ que pueda aparecer en una derivación desde el símbolo de arranque inmediatamente a continuación de la variable es susceptible de ser visto cuando se esta analizando y se aplicó $A \rightarrow \gamma$ con $\gamma \stackrel{*}{\Longrightarrow} \epsilon$ . Esto nos lleva a la definición del conjunto como conjunto de terminales que pueden aparecer a continuación de en una derivación desde el símbolo de arranque:

Definición 33.6.2 Dada una gramática $G =(\Sigma,V,P,S)$ y una variable $A \in V$ se define el conjunto como:

$FOLLOW(A) = \left \{ b \in \Sigma : \exists S \stackrel{*}{\Longrightarrow} \alpha A b \beta \right \} \cup E(A)$

donde

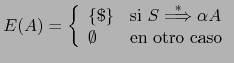
$E(A) = \left \{ \begin{array}{ll} \{ \$ \}& \mbox{si $S \stackrel{*}{\Longrightarrow} \alpha A$} \\ \emptyset & \mbox{en otro caso} \end{array} \right.$

Aqui $\$$ denota el final de la entrada (que se corresponde en el código Perl anterior con el terminal EOI).

Si $A \rightarrow \gamma_1 \mid \ldots \mid \gamma_n$ dado que los conjuntos $FIRST(\gamma_i)$ han de ser disjuntos para que un analizador predictivo APDR funcione, sólo una parte derecha puede contener la palabra vacía en su . Supongamos que es $\gamma_n$ . Podemos reformular la construcción del procedimiento para la variable siguiendo este seudocódigo:

sub A {
  if ($lookahead in FIRST(gamma_1)) { imitar gamma_1 }
  elsif ($lookahead in FIRST(gamma_2)) { imitar gamma_2 }
  ...
  else ($lookahead in FIRST(gamma_n) or $lookahead in FOLLOW(A)) { imitar gamma_n }
}

Un caso particular de $\gamma_n \stackrel{*}{\Longrightarrow} \epsilon$ es que $\gamma_n = \epsilon$ . En tal caso, y como es obvio, el significado de imitar gamma_n es equivalente a ejecutar una sentencia vacía.

Construcción de los conjuntos de Primeros y Siguientes

Algoritmo 33.6.1 Construcción de los conjuntos

Repita el siguiente conjunto de reglas hasta que no se puedan añadir mas símbolos terminales o a ningún conjunto :

$Si X \in \Sigma entonces FIRST(X) = {X}$
$Si X \rightarrow \epsilon entonces FIRST(X) = FIRST(X) \cup \{ \epsilon \}$
$Si X \in V y X \rightarrow Y_1 Y_2 \cdots Y_k \in P entonces$

$\displaystyle i = 1;$

$\displaystyle hacer$

$\displaystyle FIRST(X) = FIRST(X) \cup FIRST^*(Y_i);$

$\displaystyle i++;$

$\displaystyle mientras (i \leq k y \epsilon \in FIRST(Y_i))$
Añadir $\epsilon$ a si $i \geq k$ y $\epsilon \in FIRST(Y_k)$

Aqui

denota al conjunto $FIRST(Y) - \{ \epsilon \}$ .

Este algoritmo puede ser extendido para calcular $FIRST(\alpha)$ para $\alpha = X_1 X_2 \cdots X_n \in (V \cup \Sigma)^*$ . El esquema es anólogo al de un símbolo individual.

Algoritmo 33.6.2 Construcción del conjunto $FIRST(\alpha)$

Repita siguiente conjunto de reglas hasta que no se puedan añadir mas símbolos terminales o a ningún conjunto $FIRST(\alpha)$ :

		$\displaystyle i = 1;$
		$\displaystyle FIRST(\alpha) = \emptyset;$
		$\displaystyle hacer$
		$\displaystyle FIRST(\alpha) = FIRST(\alpha) \cup FIRST^*(X_i);$
		$\displaystyle i++;$
		$\displaystyle mientras (i \leq n y \epsilon \in FIRST(X_i))$

Algoritmo 33.6.3 Construcción de los conjuntos $FOLLOW(A) \forall A \in V$ :

Repetir los siguientes pasos hasta que ninguno de los conjuntos cambie:

$FOLLOW(S) = \{\$\}$ ( $\$$ representa el final de la entrada)
$Si A \rightarrow \alpha B \beta entonces$

$\displaystyle FOLLOW(B) = FOLLOW(B) \cup (FIRST(\beta) - \{\epsilon\})$
$Si A \rightarrow \alpha B o A \rightarrow \alpha B \beta y \epsilon \in FIRST(\beta) entonces$

$\displaystyle FOLLOW(B) = FOLLOW(B) \cup FOLLOW(A)$

Ejercicio: Construir los

Construya los conjuntos

de las partes derechas de las reglas de producción de la gramática presentada en el ejercicio 34.1.1.

Ejercicio: Calcular los

Modificamos la gramática de la sección 33.6.1 para que admita la sentencia vacía:

statements $\rightarrow$ statement ';' statements $\vert$ statement

statement $\rightarrow$ ID '=' expression $\vert$ P expression $\vert \epsilon$

expression $\rightarrow$ term '+' expression $\vert$ term

term $\rightarrow$ factor '*' term $\vert$ factor

factor $\rightarrow$ '(' expression ')' $\vert$ ID $\vert$ NUM

Calcule los conjuntos . ¿Es la nueva gramática susceptible de ser analizada por un analizador predictivo descendente recursivo? ¿Cómo sería el código para la subrutina statements?. Escríbalo.

Práctica: Construcción de los FIRST y los FOLLOW

He escrito un módulo llamado Grammar que provee la función Grammar::Parse la cual recibe una cadena conteniendo la gramática en formato yacc o eyapp y devuelve una referencia a un hash conteniendo la información pertinente para el tratamiento de la gramática. Para instalar el módulo tenga en cuenta que depende del módulo Parse::Yapp.

Para ilustrar el uso vea los ejemplos en el directorio scripts. En concreto veamos el programa grammar.pl.

Grammar/scripts$ cat -n grammar.pl
 1  #!/usr/bin/perl -w -I../lib
 2  use strict;
 3  use Grammar;
 4  use Data::Dumper;
 5
 6  sub usage {
 7    print <<"EOI";
 8  usage:
 9  $0 input_grammar
10  EOI
11    die "\n";
12  }
13
14  usage() unless @ARGV;
15  my $filename = shift;
16
17  local $/ = undef;
18  open my $FILE, "$filename";
19  my $grammar = <$FILE>;
20  my $x = Grammar::Parse($grammar);
21
22  print Dumper($x);

Vamos a darle como entrada la gramática en el fichero aSb.yp conteniendo una gramática:

Grammar/scripts$ cat -n aSb.yp
 1  %%
 2  S:
 3      |   'a' S 'b'
 4  ;
 5  %%

Las gramáticas aceptadas por Grammar::Parse se adaptan a la sintáxis de las gramáticas reconocidas por Parse::Yapp. Una gramática (normalmente con tipo .yp) consta de tres partes: la cabeza, el cuerpo y la cola. Cada una de las partes va separada de las otras por el símbolo %% en una línea aparte. Así, el %% de la línea 1 separa la cabeza del cuerpo. En la cabecera se colocan las declaraciones de terminales (directiva %token), cual es el símbolo de arranque (directiva %start), etc. El cuerpo contiene las reglas de la gramática y las acciones asociadas. Por último, la cola en nuestro caso no es usada y es vacía. En general, la cola contiene las rutinas de soporte al código que aparece en las acciones asi como, posiblemente, rutinas para el análisis léxico y el tratamiento de errores.

La salida de Grammar::Parse es una referencia a un hash cuyas entradas vienen explicadas por los comentarios.

Grammar/scripts$ grammar.pl aSb.yp
$VAR1 = {
    'SYMS' => { 'S' => 2, '"b"' => 3, '"a"' => 3 }, # Símbolo => línea
    'NULL' => { 'S' => 1 }, # símbolos que se anulan
    'RULES' => [
                 [ 'S', [] ], # S produce vacío
                 [ 'S', [ '"a"', 'S', '"b"' ] ] # S -> aSb
               ],
    'START' => 'S', # Símbolo de arranque
    'TERM' => [ '"b"', '"a"' ], # terminales /tokens
    'NTERM' => { 'S' => [ 0, 1 ] }  # índices de las reglas de las variables sintácticas
  };

Usando la estructura devuelta por la función Grammar::Parse escriba un módulo que provea funciones para computar los FIRST y los FOLLOW de las variables sintácticas de la gramática. No olvide escribir la documentación. Incluya una prueba por cada una de las gramáticas que figuran en el directorio scripts del módulo Grammar.

Puede encontrar la práctica casi hecha en PL::FirstFollow. Asegúrese de entender el algoritmo usado. Aumente el número de pruebas y haga un análisis de cubrimiento.

Gramáticas LL(1)

Una gramática $G =(\Sigma,V,P,S)$ cuyo lenguaje generado

puede ser analizado por un analizador sintáctico descendente recursivo predictivo se denomina LL(1). Una gramática es LL(1) si y sólo si para cualesquiera dos producciones $A \rightarrow \alpha$ y $A \rightarrow \beta$ de

se cumple:

$FIRST(\alpha) \cap FIRST(\beta) = \emptyset$
Si $\epsilon \in FIRST(\alpha)$ , entonces $FIRST(\alpha) \cap FOLLOW(A) = \emptyset$

¿De donde viene el nombre LL(1)? La primera L hace alusión al hecho de que el flujo de terminales se lee de izquierda a derecha, accediendo a la entrada por su izquierda (Left). La segunda L se refiere a que el método de análisis predictivo construye una derivación a izquierdas. El número entre paréntesis indica el número de terminales que debemos consultar para decidir que regla de producción se aplica. Asi, en una gramática LL(2) la decisión final de que producción elegir se hace consultando los dos terminales a la entrada.

Ejercicio: Caracterización de una gramática LL(1)

Cuando se dice que una gramática es LL(1) si, y sólo si:

$FIRST(\alpha) \cap FIRST(\beta) = \emptyset$
Si $\epsilon \in FIRST(\alpha)$ , entonces $FIRST(\alpha) \cap FOLLOW(A) = \emptyset$

se asume que los conjuntos $FIRST(\alpha)$ no son vacíos.

¿Que se puede decir de la regla $A \rightarrow \alpha$ si $FIRST(\alpha) = \emptyset$ ?
¿Que se puede decir de la variable si $FOLLOW(A) = \emptyset$ ?

Ejercicio: Ambiguedad y LL(1)

¿Puede una gramática LL(1) ser ambigua?. Razone su respuesta.

Práctica: Un analizador APDR

Siguiendo con la construcción del compilador para el lenguaje Tutu, escriba un analizador APDR para la siguiente gramática. Reutilice el código de las prácticas de las secciones anteriores (33.3 y 33.4).

program $\rightarrow$ declarations statements $\vert$ statements

declarations $\rightarrow$ declaration ';' declarations $\vert$ declaration ';'

declaration $\rightarrow$ INT idlist $\vert$ STRING idlist

statements $\rightarrow$ statement ';' statements $\vert$ statement

statement $\rightarrow$ ID '=' expression $\vert$ P expression $\vert \epsilon$

expression $\rightarrow$ term '+' expression $\vert$ term

term $\rightarrow$ factor '*' term $\vert$ factor

factor $\rightarrow$ '(' expression ')' $\vert$ ID $\vert$ NUM $\vert$ STR

idlist $\rightarrow$ ID ',' idlist $\vert$ ID

Práctica: Generación Automática de Analizadores Predictivos

Objetivo

Escriba un módulo GAP.pm que provea una subrutina gap para la generación automática de un APDR supuesto que la gramática de entrada es LL(1).

La subrutina gap recibe como entrada la gramática según la estructura de datos generada por la función Grammar::Parse de la versión 0.3 del módulo Grammar.

El Módulo `Grammar`

La estructura de datos generada por la función Grammar::Parse se explicó en la práctica 33.6.8. La estructura ha sido extendida en esta versión para incluir el código que se sitúe en la zona de cola. Por ejemplo, dada la gramática de entrada:

  Grammar/03/scripts$ cat -n aSb.yp
       1  %%
       2  S:
       3      |   'a' S 'b'
       4  ;
       5  %%
       6
       7  sub Lex {
       8    local $_ = shift; # input
       9    my @tokens;
      10
      11
      12    while ($_) {
      13      s/^\s*//; # fuera blancos
      14      push @tokens, $1, $1 if s/^(.)//s
      15    }
      16    @tokens;
      17  }
      18
      19  sub main {
      20    my $filename = shift;
      21    my $input;
      22
      23    if (defined($filename)) {
      24      local $/ = undef;
      25      open my $FILE, $filename or die "No se pudo abrir $filename\n";
      26      $input = <$FILE>;
      27      close($FILE);
      28    }
      29    else { $input = <STDIN> }
      30
      31    my @tokens = Lex($input);
      32    Parse(@tokens); # Llamada al analizador generado
      33    print "Sintácticamente correcto\n";
      34  }

se genera la siguiente estructura de datos:

{
  'SYMS' => { 'S' => 2, 'b' => 3, 'a' => 3 },  # Símbolo => línea de aparición
  'NULL' => { 'S' => 1 }, # Símbolos que se anulan
  'RULES' => [ # Reglas 
               [ 'S', [] ], # S produce vacío
               [ 'S', [ 'a', 'S', 'b' ] ] # S-> a S b
             ],
  'START' => 'S', # Símbolo de arranque
  'TERM' => [ 'b', 'a' ], # Terminales
  'NTERM' => { 'S' => [ 0, 1 ] } # Variables sintácticas e índices de las reglas de esa variable
  'TAIL' => [ # [ 'Código de cola', línea en la que está el segundo %% ]
  '

  sub Lex {
    local $_ = shift; # input
    my @tokens;


    while ($_) {
      s/^\\s*//; # fuera blancos
      push @tokens, $1, $1 if s/^(.)//s
    }
    @tokens;
  }

  sub main {
    my $filename = shift;
    my $input;

    if (defined($filename)) {
      local $/ = undef;
      open my $FILE, $filename or die "No se pudo abrir $filename\\n";
      $input = <$FILE>;
      close($FILE);
    }
    else { $input = <STDIN> }

    my @tokens = Lex($input);
    my $ok = Parse(@tokens); # Llamada al analizador generado
    print "Sintácticamente correcto\\n" if $ok;
  }

  ', 5 ], # línea en la que está el segundo %%
 };

Asi pues la entrada con clave TAIL contiene el código auxiliar de cola. Este código debe ser incluido por su programa dentro del texto del paquete generado por gap.

Descripción del objetivo: La función `gap`

La función gap también recibe como entrada el nombre del package:

$package_text = &gap($grammar, 'Package_name');

La función gap retorna una cadena conteniendo el package en el que estan las subrutinas del analizador sintáctico.

La idea es que dicha cadena se salvará en un fichero con nombre Package_name.pm que podrá posteriormente ser usado (use Package_name) por un programa que necesite analizar entradas que se conforman de acuerdo a la especificación de la gramática.

Descripción del objetivo: La función `parser`

La rutina principal del paquete generado se ha de llamar parser (esto es, su nombre completo es: Package_name::parser. Evidentemente Package_name debe ser un nombre Perl válido). Ninguna subrutina deberá ser exportada sino que deberán ser llamadas por su nombre completo.

La subrutina parser recibe como argumento el array de terminales, obtiene el primer terminal y llama a la subrutina asociada con el símbolo de arranque. Los terminales están representados como parejas .

Observe que, una vez que la cadena $package_text conteniendo el paquete ha sido generada y salvada en un fichero con nombre Package_name.pm, podemos escribir un programa cliente:

use strict;
use Package_name;

&Package_name::main;

Este programa espera una entrada desde fichero o STDIN e informa si dicha entrada es sintácticamente correcta o no para la gramática en cuestión.

Cálculo de los First y los Follow con `PL::FirstFollow`

Para facilitar la escritura de GAP.pm pueden hacer uso del módulo PL::FirstFollow el cual calcula los y los . El módulo PL::FirstFollow depende de Set::Scalar escrito por Jarkko Hietaniemi: instálelo primero.

Deberá familiarizarse con PL::FirstFollow, rellenar la documentación de todas las subrutinas (apariciones de ???? en el texto) y escribir la documentación siguiendo el template que se provee. Rellene los fragmentos de código que se han sustituido por signos de interrogación. Haga un estudio de cubrimiento y añada pruebas para mejorar el actual. El actual cubrimiento es:

---------------------------- ------ ------ ------ ------ ------ ------ ------
File                           stmt   bran   cond    sub    pod   time  total
---------------------------- ------ ------ ------ ------ ------ ------ ------
...ammar-0.03/lib/Grammar.pm  100.0    n/a    n/a  100.0    0.0   75.3   97.2
blib/lib/PL/FirstFollow.pm    100.0   92.9   50.0  100.0    0.0   24.7   95.1
Total                         100.0   92.9   50.0  100.0    0.0  100.0   95.5
---------------------------- ------ ------ ------ ------ ------ ------ ------

Si observa un fallo en PL::FirstFollow háganoslo saber y además de resolverlo escriba una prueba para detectar el fallo.

Haga un estudio de profiling de su aplicación.

Uso de Templates

Un módulo que puede facilitar la escritura de esta práctica es Text::Template debido a Mark Jason Dominus. El siguiente ejemplo de uso es un fragmento de un traductor - que nunca acabo de terminar - que toma con fuente un fichero en el formato que usa Moodle para los cuestionarios (conocido como formato GIFT) y lo convierte en un cuestionario L^ATEX:

lhp@nereida:~/projects/Gift2LaTeX/Gift2LaTeX/lib$ cat -n Gift2LaTeX.pm
   1  package Gift2LaTeX;
   2
   3  use strict;
   4  use warnings;
   5  use Gift;
   6  use Text::Template;
   7  use HTML::Latex;
  ..    ......................................................
  49  package Gift::TRUEFALSE; # True-false questions belong to this class
  50
  51  { # closure
  52
  53    die "Can't find $TEMPLATE_DIR/TRUEFALSE_question.tep\n"
  54          unless -e "$TEMPLATE_DIR/TRUEFALSE_question.tep";
  55    my $tfq_tmpl = Text::Template->new( #tfq = true-false question
  56      DELIMITERS => ['%<', '%>'];
  57      SOURCE => "$TEMPLATE_DIR/TRUEFALSE_question.tep",
  58    );
  ..    ......................................................
  67    sub gen_latex {
  68      my $self = shift;
  69
  70      ########## Generate latex for question
  71      my $prefix  = $self->PREFIX;
  72
  73      my $sufix = $self->POSTSTATE;
  74
  75      $self->Error("Only HTML and PLAIN formats are supported\n")
  76          unless (!$self->FORMAT or ($self->FORMAT =~ m{html|plain}i));
  77
  78      my ($prefix_tex, $sufix_tex);
  79      if (defined($self->FORMAT) and $self->FORMAT =~ m{plain}i) {
  80        $prefix_tex = $prefix;
  81        $sufix_tex  = $sufix;
  82      }
  83      else { # HTML by default
  ..    ......................................................
  86      }
  87      my $params = {
  88        prefix  => $prefix_tex,
  89        sufix   => $sufix_tex,
  90        separator => $separator,
  91        label   => $label_prefix.$question_number,
  92        question_number => $question_number
  93      };
  94      my $question_tex = $tfq_tmpl->fill_in(HASH => $params);
  96      ########## Generate latex for answer
 ...      ....................................
 101    }
 102  }

En la línea 55 se crea el template. El template se lee desde el fichero "$TEMPLATE_DIR/TRUEFALSE_question.tep" cuyo contenido es una mezcla de texto (en este caso texto L^ATEX y HTML) con código Perl: El código Perl aparece acotado entre los delimitadores '%<' y '%>'.

lhp@nereida:~/projects/Gift2LaTeX/Gift2LaTeX/etc/en$ cat -n TRUEFALSE_question.tep
 1  \ begin{latexonly}
 2    %<$separator%>
 3    \ label{question:%<$label%>}
 4    %<$prefix%>
 5
 6    \ begin{center}
 7      \ begin{tabular}{llll}
 8          $\ bigcirc$ & TRUE & $\ bigcirc$ & FALSE
 9      \ end{tabular}
10
11      \noindent %<$sufix%>
12    \ end{center}
13  \ end{latexonly}
14
15  \ begin{htmlonly}
16  %<$separator%>
17  \ label{question:%<$label%>}
18  %<$prefix%>
19
20  \ begin{center}
21    \ begin{tabular}{llll}
22        \ htmlref{$\bigcirc$}{answer:%<$label%>} & TRUE &
23        \ htmlref{$\bigcirc$}{answer:%<$label%>} & FALSE
24    \ end{tabular}
25
26    \ noindent %<$sufix%>
27  \ end{center}
28  \ end{htmlonly}

El template se rellena en las líneas 87-94. En esa llamada se ejecuta el código Perl incrustado en el esqueleto y su resultado se inserta en la posición que ocupa en el texto.

Concatenación y Documentos `HERE`

Cuando concatene sangre adecuadamente las concatenaciones:

my $usage = "Usage: $0 <file> [-full] [-o] [-beans]\n"
            . "Options:\n"
            . "    -full  : produce a full dump\n"
            . "    -o     : dump in octal\n"
            . "    -beans : source is Java\n"
            ;

ponga el punto al principio de la siguiente línea, no al final.

Pero cuando el número de líneas es grande es mejor usar un here document o documento aqui. Veamos un ejemplo:

print <<"EOI";
El programa se deberá ejecutar con:

$0 numfiles $opciones initialvalue
EOI

Para definir un ``documento aqui'' se escribe la etiqueta entrecomillada y precedida de << y sigue el texto que consituye el here document que se delimita por una línea en blanco que empieza por la etiqueta. Al documento aquí se le trata como una cadena de doble comilla si la etiqueta aparece en doble comilla y como de comilla simple si la etiqueta esta entre comillas simples. Observe que el punto y coma se escribe despues de la primera aparición de la etiqueta.

Un problema con el uso de los heredoc es que rompen la estructura normal del sangrado:

if ($usage_error) {
    warn <<'END_USAGE';
Usage: qdump <file> [-full] [-o] [-beans]
Options:
    -full  : produce a full dump
    -o     : dump in octal
    -beans : source is Java
END_USAGE
}

Es mejor que cada heredoc se aisle en una subrutina y se parametrice con las variables que van a ser interpoladas:

sub build_usage {
    my ($prog_name, $file_name) = @_;

    return <<"END_USAGE";
Usage: $prog_name $file_name [-full] [-o] [-beans]
Options:
    -full  : produce a full dump
    -o     : dump in octal
    -beans : source is Java
END_USAGE
}

que mas tarde puede ser llamado con los valores de interpolación adecuados:

if ($usage_error) {
    warn build_usage($PROGRAM_NAME, $requested_file);
}

Véase el libro de Conway Perl Best Practices [] para mas detalles sobre buenas prácticas de programación con heredocs.

Descarga de los Módulos Necesarios

El módulo Grammar : http://nereida.deioc.ull.es/˜pl/perlexamples/Grammar-0.03.tar.gz
El módulo PL::FirstFollow : http://nereida.deioc.ull.es/˜pl/perlexamples/PL-FirstFollow-0.02.tar.gz

Casiano Rodríguez León
2013-04-23

		$\displaystyle i = 1;$
		$\displaystyle hacer$
		$\displaystyle FIRST(X) = FIRST(X) \cup FIRST^*(Y_i);$
		$\displaystyle i++;$
		$\displaystyle mientras (i \leq k y \epsilon \in FIRST(Y_i))$